Sen(Qian)’s Memo

https://proceedings.neurips.cc/paper/2017/hash/7cce53cf90577442771720a370c3c723-Abstract.html

先行研究では、📄2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data 、📄2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data 、📄2016-NIPS-Theoretical Comparisons of Positive-Unlabeled Learning against Positive-Negative Learning のようにCost-sensitiveな手法は大きな改善を導いた。

しかし、表現力が高いモデル=DNNなどでは、経験損失が負になってしまうという問題が発生する。損失関数に上界が存在しない場合、PUの導いてきた式で負項が非常に小さく、その結果全体でマイナスになってしまうことがある。この研究は、経験損失の下限が非負にならないように、clipした。

📄2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data と同じ

そして、ここではCase Control、Positiveは$p_P(x)$の分布から、Unlabeledは$p_U(x)$の分布からそれぞれ独立にサンプリングする。

先行研究📄2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data により、以下のように計算することができる。損失関数$l(\cdot)$は負の数を受け取ると正の損失を返し、正の数を受け取ると基本0(非負)となる。

これについて、対称的な損失やHinge損失などは式変形をすると定数項を作れることによって、凸最適化されやすいという特徴があるのが2014, 2015, 📄2017-MLJ-Class-prior Estimation for Learning from Positive and Unlabeled Data だった。

これらについて、PU Learningの収束するオーダーは$O(1/\sqrt{n_P} + 1/\sqrt{n_U})$である

関数について、以下のようにノルムを考えられる。つまり、すべての値について関数のp乗を積分し割ったものである。

L∞ノルムならば、以下のようになる。

識別器のクラス$g \in \mathcal{G}$のL∞ノルムが常に有界ならば、Rademacher複雑度$\mathcal{R}(G)=O(1)$となり、サンプルの数などに影響はされない。ノルムが有界である識別器の例としては、とりうる重みに制約がかかっている場合。

そして、$l$は上限がなければ、上の定義した$R(g)$は、マイナスの項で大きい絶対値を引くと経験損失がマイナスになり、最終的にマイナス無限大へ$R(g)$は発散してしまうということになる。これは特にモデルが表現力高い=DNNのようなもので起きる。

というわけで、Non-negative Risk Estimatorを提案する。

ここでは特に、以下の部分を非負にしている。

Positiveのデータ分布に対して、ラベルがNegativeだとみなした時に招く損失が大きいほど、$- \pi \mathbb{E}_P[l(-g(\mathbf{x}))]$が最適化をする上で小さくなる。DNNのような高い学習力を持つものは、これが小さくなるように学習できて「しまう」から、問題が起きたといえる。

実際では、$\pi \cdot \sup_t \max_y l(t,y) \geq \beta \geq 0$を用いて、

• 損失が$- \beta$を上回るのならばそのまま全体の損失関数で勾配降下法で計算する。
• 損失が$- \beta$を下回るのならば、過学習していることになる。負の数を導く項のGradientを逆向きにして、ある減衰率$0 \leq \gamma \leq 1$を乗じて更新する。つまり、Gradient Ascentを行うことで過学習を防いでいる。

これによって通常のnnPUのみならず、一定量より小さいというのも実現できる。

略

DNNは6層のMLPを使用して、ReLUを活性化関数に使った。

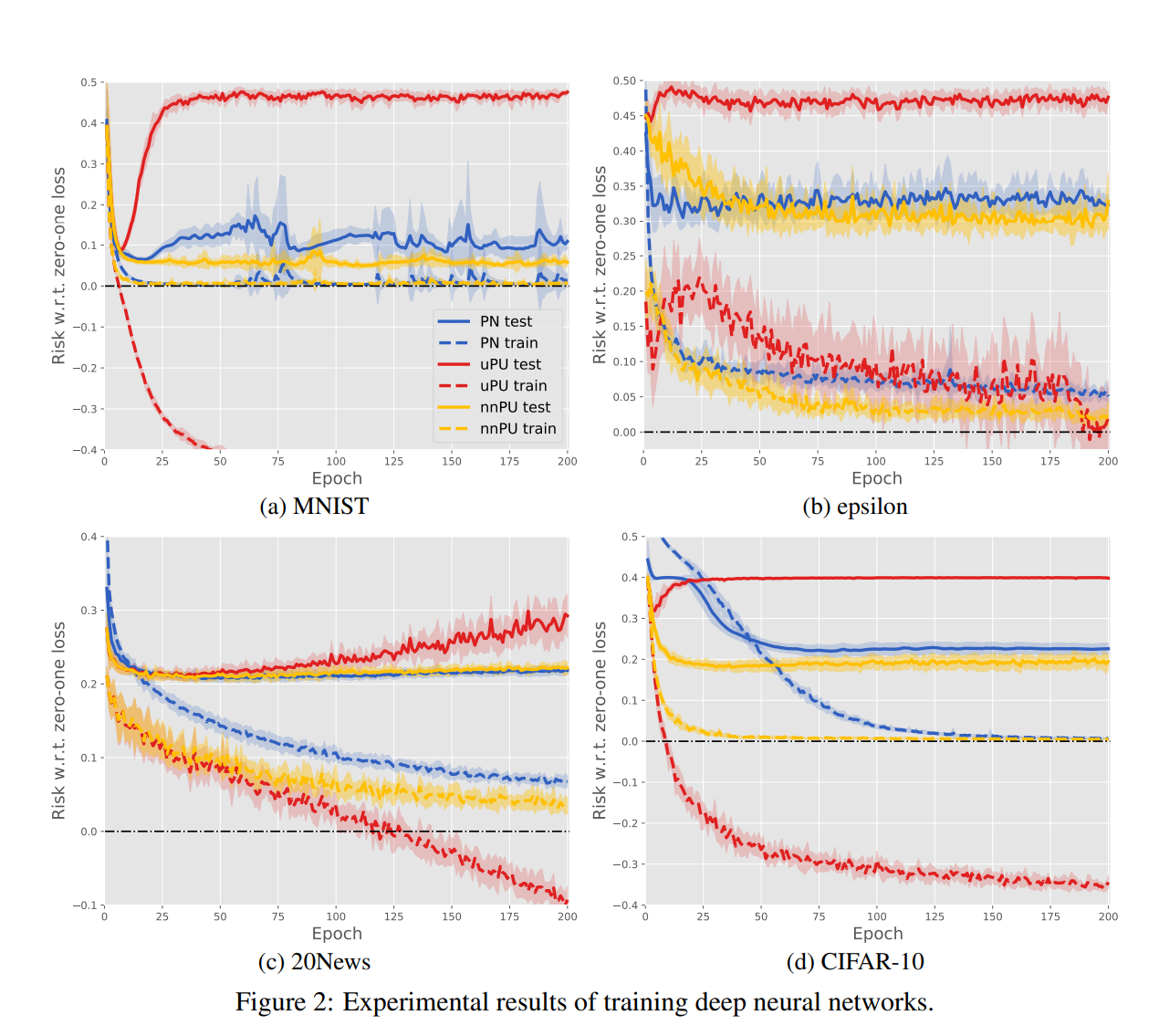
深層学習で訓練すると、高い表現力によって

• 既存のPNはだいたい問題なく、訓練損失は正となる。
• しかし 📄2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data の手法をDNNに使ったら、多くの場合で訓練損失がマイナスに発散し、テスト損失は高止まりする=過学習が起きていた。
• 提案したnnPUでは、これを防ぐことができている。

次に、真のClass PriorからずれたClass Priorに設定して実験を行った。0.8から1.2倍まで変動させた。

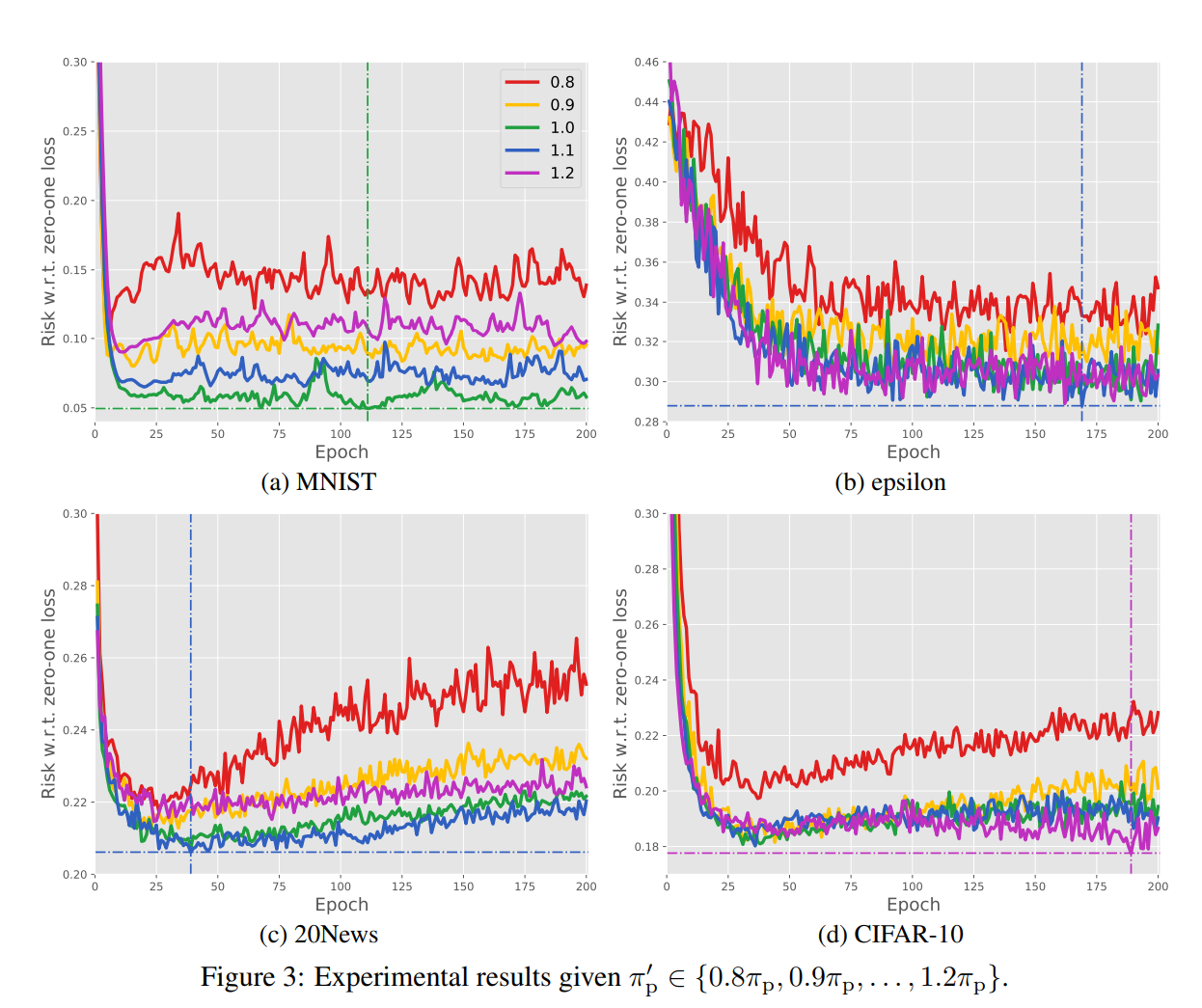
Class Priorを過小評価することはより性能を低下させるが、過大評価する場合は低下するがあｍだマシという結果になった。

Class Priorは既存の分布からの判定だと実は過大評価していたという話もあいまって、よかったですね。 → 📄2017-MLJ-Class-prior Estimation for Learning from Positive and Unlabeled Data